RxJS的响应式原理
基于RxJS构建的流式应用,能够通过一种响应式的方式构建前端复杂数据层,带来了不一样的编程思路。今天记录一下对于其响应式原理的理解,如有理解错误的地方还望指出,非常感谢。
学习要紧,但是想过儿童节
# 整体认识
RxJS是以Observable可观测数据管道为统一的IO monad,构建的异步函数式库,懂了吧,蒙了吧。蒙了没关系,老实说网上有很多说法开始我也是真的看不明白。
经过对于函数式编程范式的摸索,以及网上对于RxJS最佳实践的案例,久而久之,形成了我对RxJS内部机制的理解:
- 它实现了一种对各种数据来源的惰性推送方式,并且通过其构造的各类数据操作符Operator对流经的数据做控制
- 它是函数式编程与响应式编程的结合
- 函数式编程中构造异步的关键是惰性求值
我们将这些知识分解,一个一个讨论。
# 数据的通信方式
为什么说RxJS实现了一种对各种数据来源的惰性推送方式呢?我们先来看看js中的数据通信方式。
# 推送与拉取
这两个词来源于生产消费模型,消费者向生产者请求消费数据叫做拉取,消费者是主动的,生产者是被动的;反过来生产者主动向消费者推送产生的数据叫做推送,生产者是主动的,消费者是被动的。
在js的世界里,function都是拉取体系,在调用的时候消费传入的参数,并且只返回一个结果;迭代器(Generator)也是拉取,并且是惰性的返回多个结果。
ES6引入了Promise机制,它是一种推送的方式,在其内部响应resolve之后将数据推送出来供消费者使用,Promise的最终决议无论是resolve还是reject都只有一次;而反观Observable,它和Promise很像,在函数式编程范式中都属于monad,而不同的是Observable的返回值可以是一次也可以是多次,这是一种主动发射多次数据的机制。
了解了RxJS的数据通信方式,我们再来看看推送与拉取在前端的应用场景。
# 场景
假设某个组件内使用的一份数据x,它依赖于数据a、b、c,我们可以写出数据流向的表达式:
x = a + b + c
注意:
这里的 + 加号,指的是数据的组合关系,并不是数学意义上的加法!
现在我们讨论一下组件对于这份数据的更新,在推送与拉取不同的通信方式下的表现:
- 如果是拉取,则是在组件使用到这份数据
x的时候,去获取a、b、c三个依赖数据的当前值,组合成数据x传入组件内。这种方式的优点是十分的便利,只需要处理这一份数据关系,即x = a + b + c就可以了,缺点是无法做数据的缓存处理,拉取的时候并不知道a、b、c是否发生过改变,只能是一并获取当前值。 - 如果是推送,则是在
a、b、c任意一个数据发生变化的时候推送至组件,完成x的更新。优点是关注点分离,并且是高响应的,缺点则是需要同时维护三分数据的关联关系,即x1 = a1 + b + c、x2 = a + b1 + c、x3 = a + b + c1,成本高。
这两种方式各有优劣,那么有没有什么办法,能够既拥有推送形式的高响应性,又能够只维护一份数据关联关系呢?答案是肯定的!
通过搭建 可观测的数据管道(Observables) ,能够构建响应式的数据流 $a、$b、$c ,形成 $x = $a + $b + $c 的数据管道,当其中任意一条数据流发生变化,便会顺着 $a + $b + $c 的数据管道流入 $x 触发更新操作,就好像一条条水管,里面的水流可以观测,在流动的水流(数据更新时)流经的所有管道内(与之相关联的数据分支)处理业务逻辑。
这种形拉实推的数据通信方式,使得我们能够以一种流动的数据的方式构建响应式应用。并且通过这种方式构建的应用,业务逻辑清晰可见、拓展性良好,是构建前端复杂数据逻辑层的利器。
tip:
其实在有些前端框架中实现了这种形拉实推的方式,通过框架内部实现的一套机制,维护一份数据的相关依赖,在依赖更新的时候主动触发更新这份数据。Vue中的 computed 计算属性就是很好的例子,这种实现方式在某些场景下用起来非常方便顺手,但是当数据逻辑过于复杂,亦或是存在异步的数据更新,这种方式就不适用了。
# 函数式编程范式
刚刚我们讨论的数据通信正是一种响应式的思考方式,它关注的是构建数据之间的关联关系,然而光有这些虚无缥缈的理论还是远远不够的,我们更关心在js中应该如何创建这些个数据管道呢?RxJS是函数式编程与响应式编程的结合又如何理解呢?不着急,我们需要先对函数式编程有个基本认识。
我们知道函数式编程范式的宗旨是声明式的构建纯函数操作数据,同样的输入一定会得到同样的结果(跟数学里的函数很像),不产生副作用等等。它将构建一个应用程序的对数据的操作高度抽象成一个个手术刀级别的纯函数方法,方便组合和复用,之后的工作就像组装高达一样,将一个个零部件拼接在一起,最终形成一个结构完整的应用。
这里再讨论一下关于声明式和命令式在代码可读性方面的问题:
- 命令式的代码在于描述详细的操作步骤告诉计算机该怎么做,这是一种比较底层细节的描述形式,像
if语句和for循环这样的语句,这些语句旨在精确地指导计算机如何完成一件事情。 - 声明式的代码在于将细节做高度抽象,封装成一些声明式的操作,通过层层组合将这些操作拼在一起,构建应用程序,声明式代码更专注于描述最终的结果。
举个很形象的例子就是:
现在你要打造一辆汽车 (应用程序) ,你 (开发人员) 可以用一种将所有的零部件暴露在外,构成一个细节精致、组装结构清晰的命令式的方式;也可以用把所有零部件都隐藏在内部,将轮胎与整体车身结合的声明式的方式。这两种方式都可以打造一辆汽车,但是如果站在使用者 (同事) 的角度看待这辆汽车,他可能并不关系这辆汽车是如何打造的 (代码的具体实现细节) ,他只关心这辆车好不好用、性能以及速度如何 (封装的方法如何调用) 。所有的零部件暴露在外的方式 (命令式的代码) 反而增加了使用者的学习成本 (代码可读性) 。
这里附上声明式和命令式代码的可读性曲线:
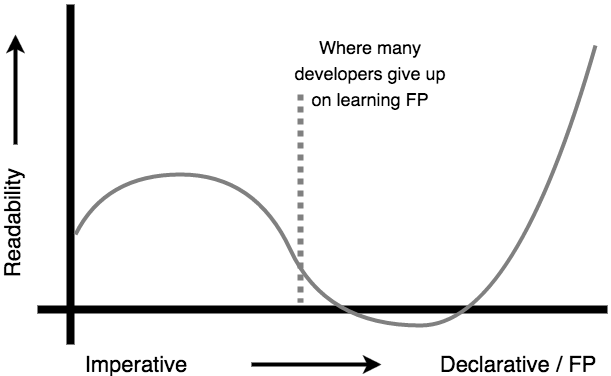
关于函数式编程的学习,推荐去看看Kyle Simpson(《You-Dont-Know-JS》作者)写的JavaScript轻量级函数式编程Functional-Light-JS。掘金上面有的译文。
安利了半天,我们回来看看我们的RxJS,为啥它的所有操作符几乎都是纯函数呢?因为对于一个应用来说,大量使用全局变量作用在业务逻辑代码中是难以维护的,想象一下如果 A 业务和 B 业务同时用到了系统状态 X ,并且都能够修改状态 X ,那么为了一个随时可能变化的状态而在业务逻辑中写大量的边界情况、异常处理,这样的代码是难以阅读的,或者说是不可信赖的(天晓得知道 A 改的这个 X1 在 B 里面会出什么乱七八糟的问题)。而RxJS中的数据管道大量充斥着同步、异步逻辑操作,如果使用了不纯的数据操作,这就违背了RxJS的设计初衷。
of, from, fromEvent, merge, interval 这些就类似于create的变形,用于生成新容器
而map, flatMap, filter相当于这些容器推送的值的操作,返回新容器
# 异步的函数式
现在我们回到刚刚的问题:在js中应该如何创建这些个数据管道呢?
在之前的描述中,我们希望数据管道的行为是响应式的,可以根据生产者提供的数据实时处理对吗?这就需要用到异步的函数式的概念。
# 积极的 vs 惰性的
积极的和惰性的在计算机科学的领域并不是表扬或者批评的意思,而是描述一个操作是否立即执行或者是延时执行。
如果只是用普通的函数式来操作数据,这些操作都是同步的、积极的:
const a = [ 1, 2, 3 ]
const b = a.map(x => x * 3)
console.log(b) // [ 3, 6, 9 ]
// 后续的修改a的值,b不会受到影响
a.push('4')
console.log(b) // [ 3, 6, 9 ]
这里 a 到 b 的映射就是积极的,因为它在执行的那一刻映射了数组 a 里的所有的值,然后生成了一个新的数组 b ,即使后续修改 a 的值, b 也不会受到影响。
再反观我们的数据管道的行为,相当于我们需要这样一个特别的数组 a ,它能够将值可以随时的一个一个添加进去,并且需要 b 是一个懒的、惰性的 映射过程,任何 a 新添加进来的数据都经过 b 映射出来。
# js实现惰性求值
思考如何通过js将这种行为表现出来,总结一下就是:
- 需要
a作为一个数据生产者,来异步的推送数据,最简单的就是定时器。 - 需要
b能够实时响应a的数据变化,需要用到观察者模式或者是发布订阅模式。
大概就是下面这个样子:
// 生产者:
const a = {
next (v) { // 绑定观察者
b.onData( v )
}
}
setInterval( () => { // 一秒生产一次数据
a.next( Math.random() )
}, 1000 )
// **************************
// 消费者:
const b = {
map (v) {
return v * 3
},
onData (v) { // 响应 a 的变化
v = this.map( v )
console.log( v )
}
}
这样,在 a 生产新数据的时候, b 能够检测到这种变化,异步的、惰性的以一种数据流的方式映射处理,因此,函数式编程中构造异步的关键是惰性求值。并且从一个侧面反映出:此时的 b 是响应式的,这便是函数式编程与响应式编程碰撞出的火花。
# 从一个Rx的最小实现理解
说了一大堆理论,我们可以来看看这篇文章中RxJS原理解析之自己造一个,对于一个Observable的最小实现是怎么样的。
先来看看发布订阅在RxJS中的提现:
const myObservable = new Observable(
observer => {
const datasource = new DataSource();
datasource.ondata = (e) => observer.next(e); // 在这里我们看到了发布订阅模式的实现
datasource.onerror = (err) => observer.error(err);
datasource.oncomplete = () => observer.complete();
return () => {
datasource.destroy();
};
}
);
我们在初始化Observable时传入了我们的subscribe,在内部绑定数据源,当数据源发送数据的时候,我们调用observer中的next实现数据的消费。
现在来看看我们的Observable:
class Observable {
constructor(_subscribe) { // 我们在new Observable的时候传递的函数其实才是真正的subscribe
this._subscribe = _subscribe; // 保存起来当我们调用subscribe的时候回来调用他的
}
subscribe(observer) {
const safeObserver = new SafeObserver(observer);
safeObserver.unsub = this._subscribe(safeObserver);
return safeObserver.unsubscribe.bind(safeObserver);
}
}
这里仅将初始化Observable时传入的_subscribe保存在实例的属性里,当我们调用subscribe添加订阅的时候才真正开始消费生产者发送出来的数据。
接下来我们调用一下刚写的Observable就明白了:
// 假设这里已经定义了许多可用的Operator
myObservable.map(x => x * 3) // 每项映射为当前的三倍
.filter(x => x % 2 === 0) // 过滤出偶数
.take(2) // 之取出两项
setTimeout(() => {
myObservable.subscribe(x => {
console.log(x)
})
}, 5000)
看到了嘛?在我们初始化的 myObservable 上绑定了 map、filter、take 一系列操作符,但只是绑定并没有执行,只有当5秒之后我们执行 subscribe 绑定我们的订阅,整个应用才开始工作,并且绑定的操作符会作用于生产者每一次发送的数据,从而实现了惰性求值,也就是异步的函数式,也就是RxJS的响应式原理。
另外,RxJS真正强大的地方是他的数据操作符Operator,RxJS中有多达104个operators操作符,对于流入的数据进行归并、控制、分发等一系列操作,如果你对于函数式编程范式构建应用程序比较属性,那么看到这里的你应该会和我一样非常兴奋,也许完成一个用传统方式编写的功能,用上RxJS只需几行😂。
# 总结
因此我将RxJS的行为总结如下:
- 它实现了一种对各种数据来源的惰性推送方式,并且通过其构造的各类数据操作符Operator对流经的数据做控制
- 它是函数式编程与响应式编程的结合
- 函数式编程中构造异步的关键是惰性求值
希望彼此在探索路上越走越远。
# 推荐的资源
个人推荐的学习RxJS的文章,本篇博客很多知识都来源于这些文章,再次表示感谢:
# 题外话
毕业已经快一年了,工作很忙很充实,学习了很多前辈的经验,偶尔也帮同事擦擦屁股。工作中一个个需求有很对胃口的,也有比较尴尬的,但毕竟都是工作,都需要好好对待。
记得一个前辈说的,有的时候工作就真的只是工作,并不是每次都有收获,真正想要提高自己,做自己感兴趣方向的研究,是需要自己额外去花时间的。深以为然,并且非常感谢他。
